Thomas Snyder (aka Dr. Sudoku) is a three-time World Sudoku Champion and six-time US Puzzle Champion, as well as the author of several books of puzzles. His puzzles are hand-crafted, with artistic themes, serving as a kind of “cure for the common sudoku.” Almost every day he posts a new puzzle on his blog, The Art of Puzzles. This week’s prescription stretches the rules of sudoku a bit, forming an amazing classic sudoku with only nine digits!
I was on a sort of puzzle sabbatical last year (read: I was working at a biotech start-up and had no free time!). But 2012 was an interesting year for sudoku. Gary McGuire of University College Dublin and collaborators were the first to prove that a classic sudoku needs 17 givens to have a unique solution.
Well, 2013 brings the first "counter-example" from Dr. Sudoku. Of course, I had to stretch the rules quite a bit. While my puzzle has just 9 digits in it, the 5 is much larger than the others. The puzzle is somewhat hard, but should be quite enjoyable to solve.
Rules: Insert a digit from 1-9 into each cell so that no digit repeats in any row, column, or region.
Puzzle: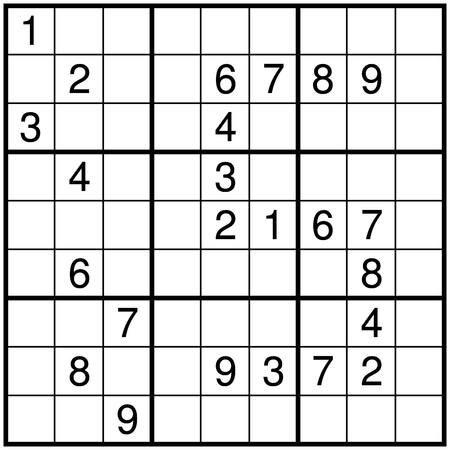
__Solution »__Solution:
