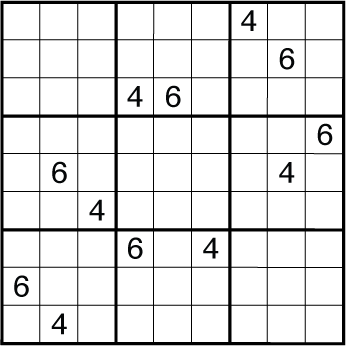
Thomas Snyder (aka Dr. Sudoku) is a two-time World Sudoku Champion and five-time US Puzzle Champion, as well as the author of several books of puzzles. His puzzles are hand-crafted, with artistic themes, serving as a kind of “cure for the common sudoku.” Each week he posts a new puzzle on his blog, The Art of Puzzles. This week’s prescription is a nonconsecutive sudoku with a twist: only two different digits appear as givens in the grid.
Nonconsecutive sudoku (where vertically and horizontally adjacent cells cannot contain consecutive numbers like 3 and 4) is amongst my favorite sudoku variants, and I've featured them in some of my past work including the book Mutant Sudoku. While it's easy to make a novelty puzzle with very few givens compared to "classic sudoku", it's harder to make a novelty puzzle that is actually fun (and possible) to solve. This week I tried to construct a two digit non-consecutive puzzle that had an interesting solution path. Enjoy!
Rules: Place a single digit from 1 to 9 into each cell so that no digit repeats in any row, column, or bold 3x3 region. No pair of consecutive digits can be placed in vertically or horizontally adjacent cells.
