Thomas Snyder (aka Dr. Sudoku) is a two-time World Sudoku Champion and five-time US Puzzle Champion, as well as the author of several books of puzzles. His puzzles are hand-crafted, with artistic themes, serving as a kind of “cure for the common sudoku.” Each week he posts a new puzzle on his blog, The Art of Puzzles. This week’s prescription deals with a variation of Kakuro (Cross-Sums) where concatenation leads to harder clue interpretation.
This weekend was the MIT Mystery Hunt. My very first hunt was in 2006 with the SPIES Hunt. It was an incredible experience and quite the introduction to the puzzle hunt scene, with my team winning after finding the hidden "coin" - a snow globe - at 12:31 AM on Sunday morning after ~36 straight hours of puzzling. In the years since, I've helped write the Hunt twice (in 2007, and 2009 - after winning again in 2008) but I sat out last year. In part because I no longer had a team; in part because I was simply a bit burned out of the whole Hunt experience which is truly a massive and challenging test of intellect and endurance, even on the "easy" years. However, I got the chance to solve remotely again this year, and this year's video game-themed Hunt was spectacular.
The Mystery Hunt is known for very difficult puzzles with zero instructions. If last week's "Mystery Puzzle" fit the zero instructions concept, then this week's puzzle probably fits the "very difficult" label. It's based on the very first Mystery Hunt puzzle I wrote for the 2007 Hunt. This time around, I'll at least give the instructions. While Mystery Hunt puzzles must embed an answer word/phrase within the puzzle, this is just a straight test of logic with nothing to find but the solved grid. Enjoy.
Instructions:
Enter a digit from 1 to 9 into each cell so that each clue accurately represents the value for some sum of the digits in the cells to the right/below the clue. Digits cannot repeat in any entry, but can repeat in a row or column in the whole grid. Unlike a standard kakuro, where a plus sign is always inserted between all adjacent digits, here a sum may be formed from multi-digit numbers after concatenation, but in each case at least one + sign must be used. In other words, a 24-clue in three cells can be satisfied by an entry like 987 (as 9+8+7 = 24) or 519 (as 5 + 19 = 24) but a 16-clue in two cells cannot be satisfied by 16, since that does not use any addition.
Example: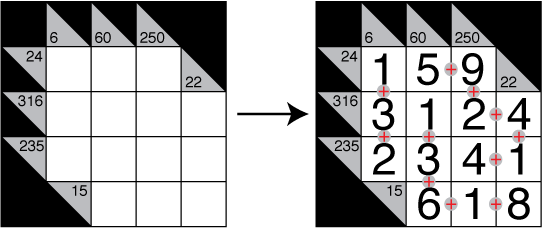
Puzzle:
